Understanding solidification and nucleation in aluminum alloys
In metallurgy, there’s a seemingly simple concept but ultimately complex process that metals undergo during a liquid-solid phase change; also termed solidification or freezing. This process refers to the nucleation and growth of the crystalline lattice grains that make up the solid structure. Many factors affect this phenomenon which define a metal’s physical and mechanical properties.
Solidification
Solidification can incur extensive supercooling, which will alter the way that the metal nucleates grains. Two types of grain nucleation can occur during solidification: homogeneous nucleation and heterogeneous nucleation. Both types of nucleation are governed by the thermodynamic quantity, Gibbs free energy, which defines a nuclei’s favorability to grow and form the crystalline lattice grains that make up the metal’s microstructure.
Gibbs free energy takes into account the enthalpy (heat) change in the system as well as the entropy (disorder) of the atoms or molecules in the system. The general equation for Gibbs free energy is Eq.1, where ΔG is the Gibbs free energy, ΔH is the enthalpy change or heat of the system, T is the temperature in Kelvin, and ΔS is the entropy change or disorder in the system.
Δ𝐺=Δ𝐻−𝑇Δ𝑆
(Eq.1)
The simple way to tell whether a thermodynamic process is favorable or not is based on the sign of change in free energy. Before the embryo achieves its critical radius and is considered a stable nuclei it may re-dissolve into the liquid. A degree of undercooling, or magnitude of temperature below its solidification temperature, decreases the size of the critical radius. The free energy change of the system becomes negative when the embryo grows larger than the critical radius, and the process is thermodynamically favorable.
During solidification both volume free energy and surface free energy are considered, with surface (interfacial) energy being positive (unfavorable) while the solid volume energy being increasingly negative (favorable) with additional undercooling. When the embryo is small the surface area-to-volume ratio is large and thermodynamically unfavorable due to excessive surface area free energy. As the embryo grows larger than the critical radius, it becomes a growing nuclei, and the favorable volume free energy overcomes the surface free energy.
Homogeneous Nucleation
Homogeneous nucleation can be described as formation of a lattice structure within the confines of a liquid. To simplify these explanations, it is assumed that the nuclei are spherical in geometric shape, as shown is Eq.2. The free energy for nucleation takes into account the free energy per unit volume (Δ𝐺𝑣), the free energy per unit area (𝛾), and the size of the embryo or nuclei. Figure 1 depicts an annotated schematic of a homogeneously nucleated crystal. The Gibbs free energy for nucleation of a spherical crystal, which is a reasonable approximation for homogeneous nucleation, is:
Δ𝐺=43𝜋𝑟3Δ𝐺𝑣+4𝜋𝑟2𝛾
(Eq.2)
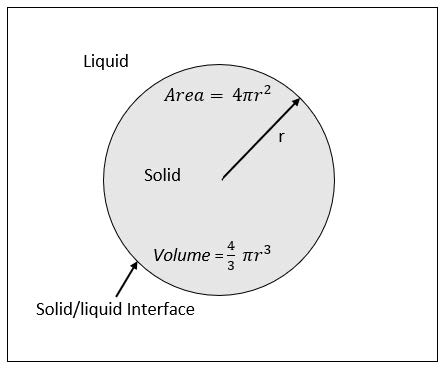
When the above equation is portrayed graphically, as in Figure 2, an activation free energy (Δ𝐺∗) is observed to be associated with a critical radius (𝑟∗), where the stability and continued growth of the nuclei becomes favorable. Typically, this is determined by differentiating EQ.2 with respect to the radius (r) and setting it equal to zero. This will give the value of the critical radius, for at this value there is no change in free energy and nuclei growth beyond size radius becomes imminent.
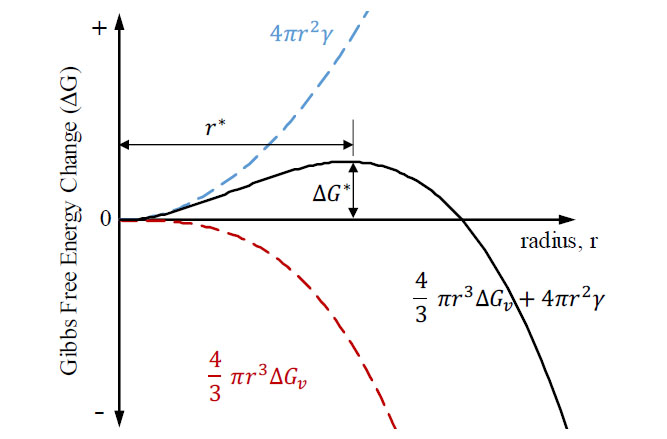
For homogeneous nucleation to occur the liquid must be significantly undercooled below its freezing temperature, up to hundreds of degrees Celsius.
Heterogeneous Nucleation
The addition of preexisting surfaces within the liquid enable the metal to readily nucleate heterogeneously with minimal undercooling. This type of nucleation occurs on preexisting surfaces, i.e. mold walls, impurities, inoculants, etc. Figure 3 expresses a conceptual model of heterogeneous nucleation on a flat surface.
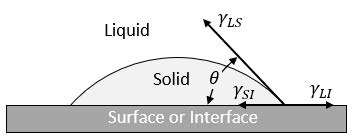
In heterogeneous nucleation, the surface energy component is a relationship between three different surface interface energies and the wetting angle (𝜃). The energies are still related to Eq.2 and can therefore be compared directly to homogenous nucleation. Figure 4 qualitatively compares the activation free energy and the critical radius of the two types of nucleation.
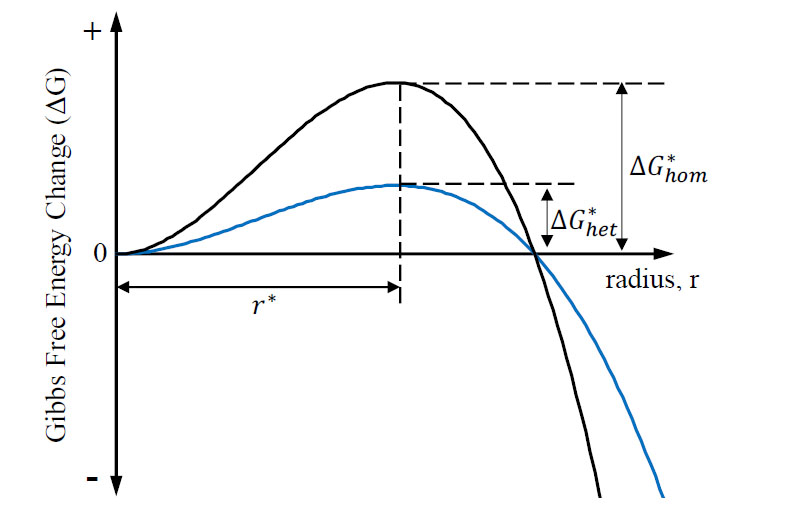
The decreased activation energy required to nucleate a grain heterogeneously explains the relative ease for this phenomenon to occur while the critical radius for nucleation is constant. Real alloy systems typically exhibit more complex solidification behavior including formation of more than one stable crystal phase.
Dendritic Solidification in Aluminum alloys
Many aluminum alloys are found to solidify in dendritic structures These structures are often times the result of larger solidification temperature ranges where primary phases are solidified first, in a dendritic or tree-like structure, while the remaining liquid in the material backfills the spaces between dendrites. Aluminum is known to have a relatively large coefficient of thermal expansion and will shrink as it solidifies and cools. Figure 5 depicts the primary dendrite formation, as commonly seen in aluminum alloys, leaving the regions between dendrites free for the remaining liquid in the system to fill. While the material cools, the solid grains begin to shrink and the solidifying secondary phases cannot adequately backfill into the voids.
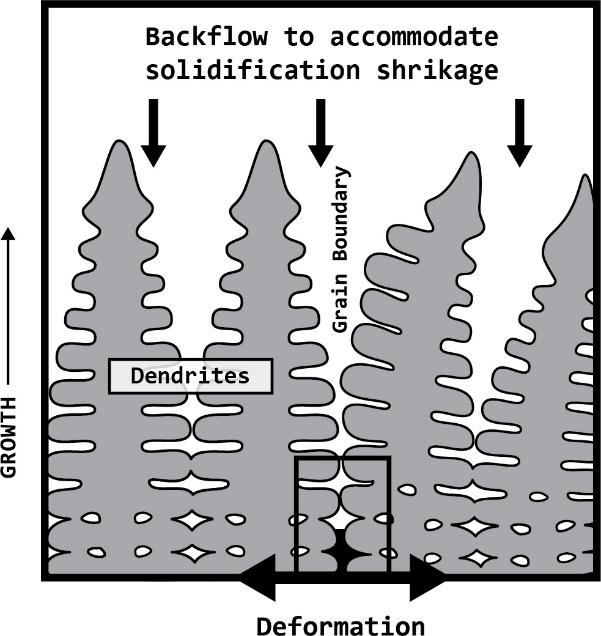
This inadequate backfill creates zipper-like porosity as the metal cools and the internal stresses from the shrinking solid overcome the strength of these weak grain boundaries resulting in cracking at the grain boundaries. This event is called hot tearing, which is a type of solidification cracking. When hot tearing occurs, the material loses many of its mechanical properties and is no longer useful for structural employment.
A solution to hot tearing in high strength aluminum alloys is the use of inoculants as heterogeneous nucleation sites. Inoculants are typically in the form of second phase particles that solidify to form a fine dispersion of heterogeneous nucleation sites while the bulk of the material is in the liquid phase. These well dispersed nucleation sites promote a fine grain structure and reduce or eliminate hot tearing.
Inoculants and Reactive Additive Manufacturing
Reactive Additive Manufacturing (RAM) utilizes exothermic chemical reactions to synthesize second phase product materials in situ during the additive processes. This RAM process can be used to produce a wide range of inoculants and is especially well suited for producing ceramic reinforced metal matrix composites (MMCs). By forming ceramic particles that act as heterogeneous nucleation sites, many unweldable and therefore ‘unprintable’ alloys, like AA6061, AA2024, and AA7050, can be made weldable and suitable for additive manufacturing (AM) processes. The process can synthesize sub-micron ceramic reinforcements from larger AM feedstock powders that are optimized for process flow, spreadability, and environmental stability [4].
Figure 6 and Figure 7 depict additively manufactured traditional AA6061 and Elementum 3D’s A6061-RAM2 materials processed by laser powder bed fusion (L-PBF). The images were produced by electron backscatter diffraction (EBSD) where grain orientations can be indexed and differentiated by a spectrum of colors. The black regions extending along the grain boundaries in Figure 6 are examples of hot tearing in the printed AA6061 material, while the more circular black regions are pores.


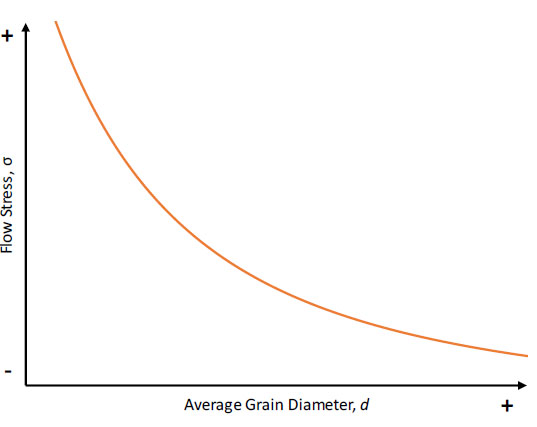
The nucleant particles also improve properties by precipitation/dispersion strengthening with the strong ceramic reinforcements acting to pin dislocation movements. The resulting fine-grained equiaxed microstructures also increase mechanical performance according to the Hall-Petch relationship. The Hall-Petch equation (Eq.3) relates a material’s average grain size to its flow stress, which is also corresponds to an increase in hardness.
𝜎=𝜎0+𝑘𝑑−12
(Eq.3)
Figure 8 expresses this concept graphically; as the average grain diameter decreases, the material’s flow stress increases. The increased strength results from increased grain boundary area which impedes the movement of dislocations through a material and increase dislocation densities.
Inoculation also produces a more equiaxed grain morphology which results in mechanical properties that are more isotropic (uniform in all directions). The equiaxed grains therefore reduce the effects of part orientation during printing on properties and in-service performance.
Elementum 3D has leveraged reactive additive manufacturing to synthesize well dispersed heterogeneous nucleation sites to produce better printable materials. Materials technology is a key enabling technology and is the first step in realizing boundary pushing product improvements and innovative new applications.
References
[1] W. D. Callister and D.G. Rethwisch, Ed., Material Science and Engineering an Introduction. 8th ed., John Wiley & Sons, 2010.
[2] R. Abbaschian, L. Abbaschian, R.E. Reed-Hill, Ed., Physical Metallurgy Principles. 4th ed., Cengage Learning, 2009.
[3] M. Rappaz, J.M. Drezet, V. Mathier, S. Vernede, “Towards a micro-macro model of hot tearing.” Material Science Forum, vol. 519-521, pp. 1665-1674, July 2006.
[4] J. Nuechterlein, J. Iten, “Reactive Additive Manufacturing” U.S. Patent Application No. 15/070,514, Sinter Print Inc., Erie CO, 2015
[5] M. Chase, “NIST—JANAF Thermochemical Tables (Journal of Physical and Chemical Reference Data Monograph No. 9),” American Institute of Physics, 1998.